Comment prédire l’état d’une machine ?

Jul 19, 2022 14 min de lecture

Prédire l’état d’une machine

Avez-vous des équipements avec des capteurs qui renvoient des informations ? Alors vous êtes déjà prêts pour l’IOT. Utilisez-vous ces données pour prédire ce qui va se passer ensuite ? Si ce n’est pas le cas, vous manquez une opportunité de tirer réellement profit de vos équipements, et nous allons voir comment vous pouvez la débloquer.

Nous allons construire un modèle capable de prédire l’état d’une machine. Nous passerons en revue 3 étapes pour résoudre ce défi en utilisant l’apprentissage automatique :

Découverte des données
Interactions
Création du modèle

À la fin, vous serez en mesure d’améliorer vos prévisions de pannes et tirer parti de vos ressources grâce à l’apprentissage automatique.

Allons-y!

Si vous envisagez de développer des capacités IOT à l’avenir ou si vous disposez déjà de machines équipées de capteurs capables de renvoyer des informations, vous êtes mûrs pour vous lancer dans ce défi.

La compétition proposée par Kaggle en mai 2022 propose un jeu de données (simulées) d’une machine, et l’objectif est de prédire l’état de la machine qui peut être en statut 0 ou 1. Nous disposons d’un jeu de données avec l’état associé, et il faut prévoir l’état pour de nouvelle données. C’est donc un problème de classification binaire, qui passe par la découverte d’interactions, par l’analyse des données, et par la création d’un modèle d’apprentissage automatique.

Je vais me servir des données de cette compétition pour montrer comment utiliser le deep learning avec Keras et R pour prédire l’état d’une machine.

Vous pouvez trouver les données à l’adresse suivante : https://www.kaggle.com/competitions/tabular-playground-series-may-2022/data

Découverte des données

Les données sont composées de 33 variables, dont le statut à prédire et un identifiant pour chaque observation.

Les données se répartissent en 3 catégories :

16 variables numériques continues
14 variables contenant des entiers qu’on va traiter en variables discrètes
1 variables alphanumérique composée d’une suite de caractères.

Il y a environ autant de données pour le statut 0 et 1, le jeu de données est donc équilibré.

Regardons la distribution des variables :

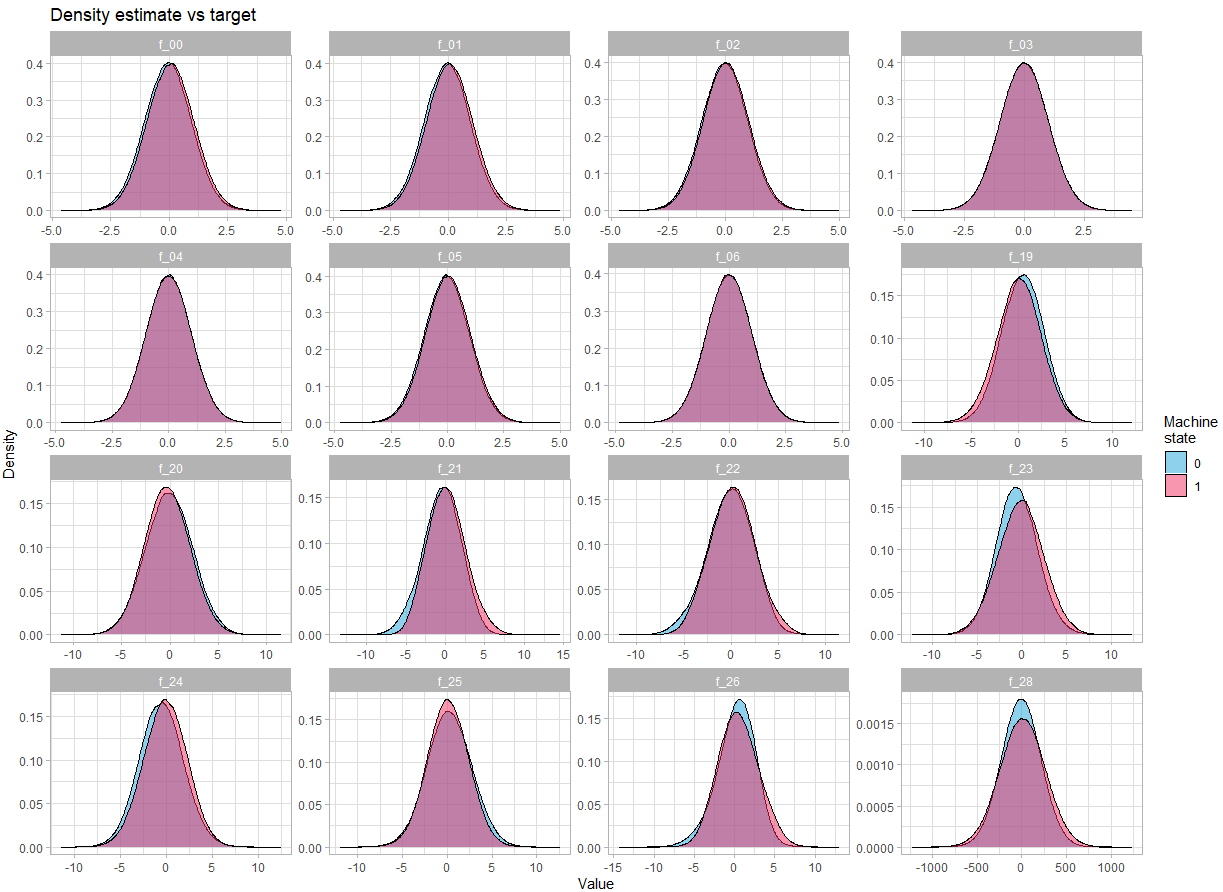
Pour les variables continues :

train |> 
  select(id, f_00:f_06, f_19:f_26, f_28, target) |> 
  mutate(target = as.factor(target)) |> 
  pivot_longer(cols = -c(id, target)) |> 
  ggplot(aes(x = value, y = ..density.., fill = target))+
  geom_density(alpha = 0.5)+
  scale_fill_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  facet_wrap(~name, scales = "free") +
  labs(title = "Density estimate vs target",
       x = "Value",
       y = "Density",
       fill = "Machine\nstate") +
  theme_light()

On constate qu’il n’y a pas une différence flagrante dans la densité en fonction de l’état de la machine.

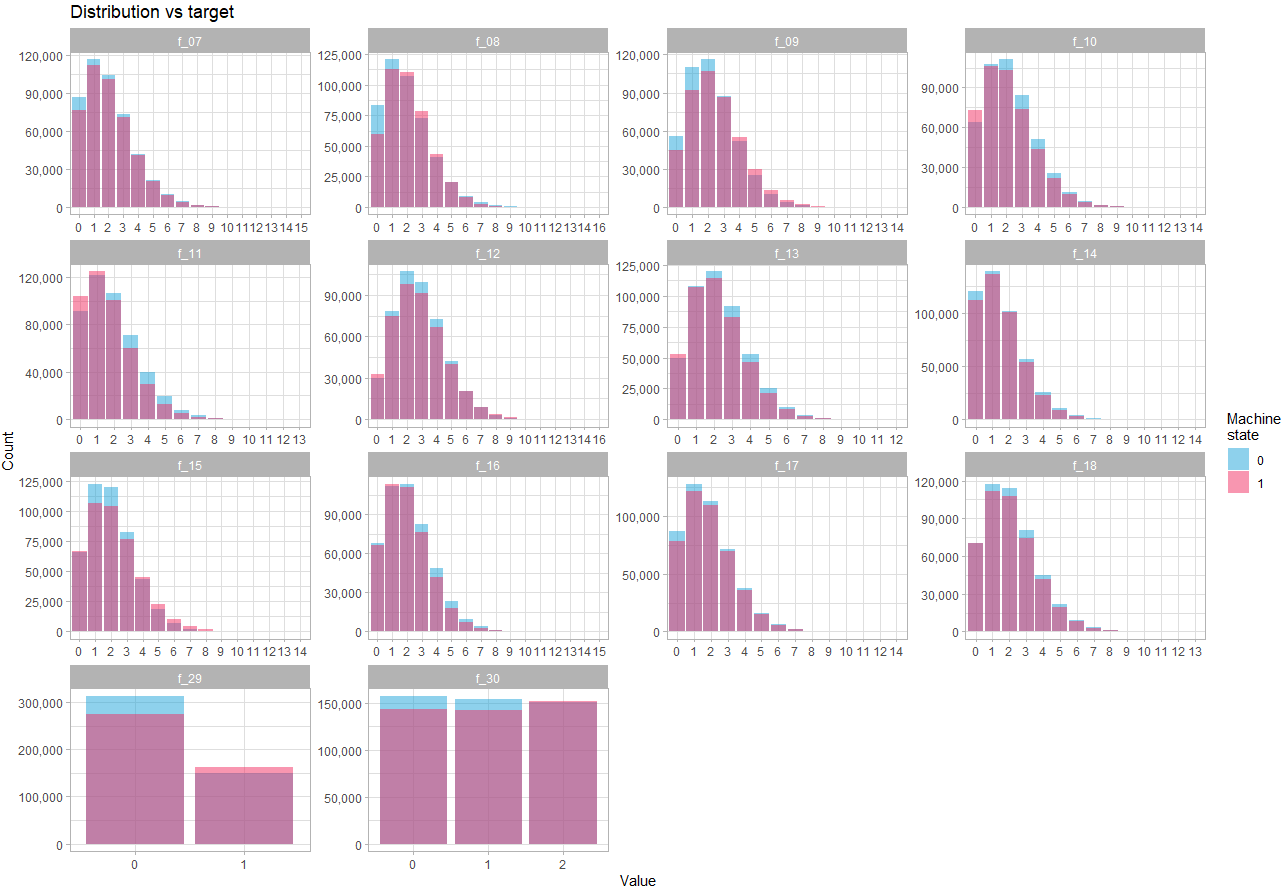
Regardons les variables discrètes :

train |> 
  select(id, f_07:f_18, f_29:f_30, target) |> 
  mutate(target = as.factor(target)) |> 
  pivot_longer(cols = -c(id, target)) |> 
  count(name, value, target) |> 
  ggplot(aes(x = value, y = n, fill = target))+
  geom_col(position = "identity", alpha = 0.5)+
  scale_fill_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  scale_y_continuous(label = scales::comma) +
  facet_wrap(~name, scales = "free") +
  labs(title = "Distribution vs target",
       x = "Value",
       y = "Count",
       fill = "Machine\nstate") +
  theme_light()

Ici on constate que la différence de distribution en fonction de l’état est assez subtile, ce qui confirme que la force de prédiction résidera dans les interactions entre variable.

La dernière variable est la f_27. Elle comprend une combinaison de lettres, et sur 900 000 observations, il y a 741354 observations distinctes. Là encore, ça ne parait pas exploitable tel quel. Mais en regardant le contenu de la variable, il apparait évident qu’elle ressemble à la concaténation de 10 variables, contenant chacune un certain nombre de lettre de l’alphabet.

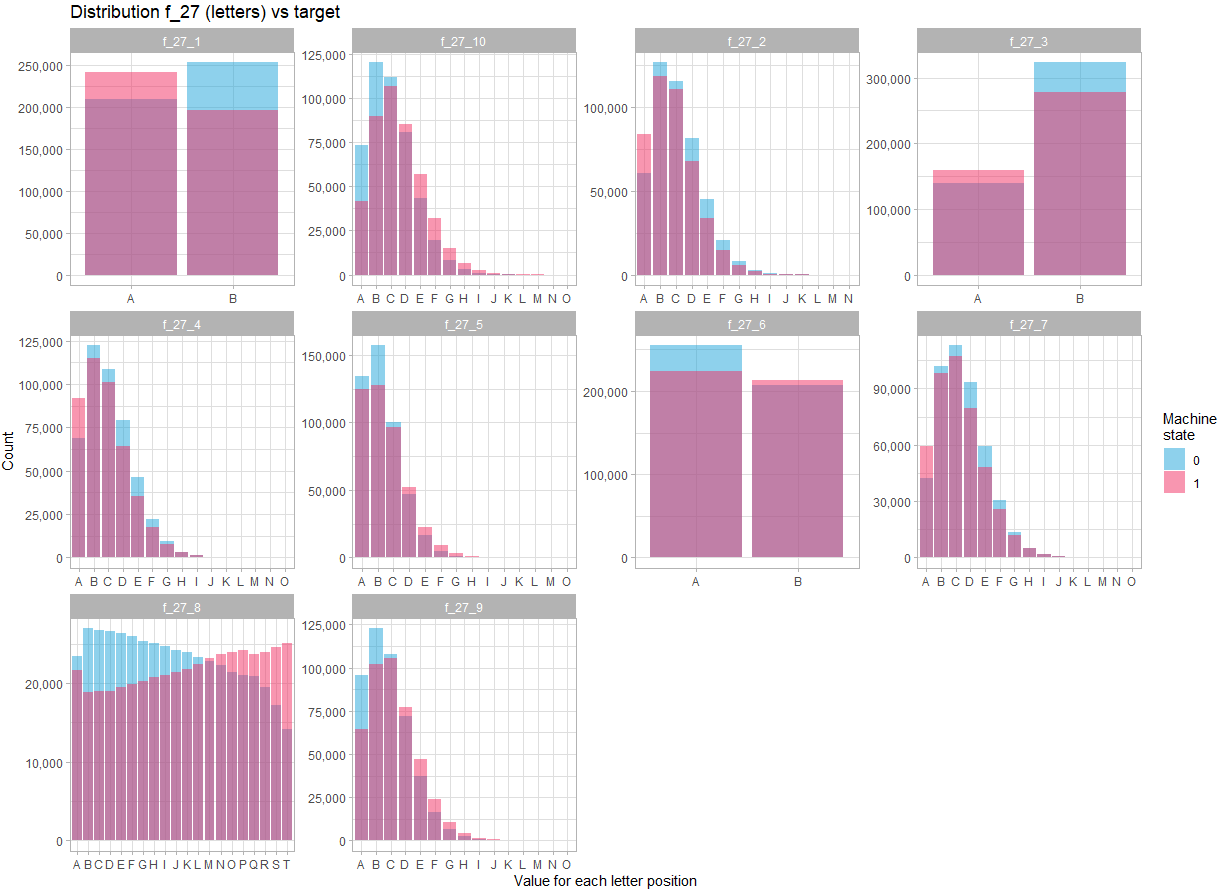
Si on séparer la variable f_27 en 10 variables, et qu’on regarde sa distribution :

train |> 
  select(target, f_27) |> 
  mutate(target = as.factor(target)) |> 
  separate(col = f_27, into = paste0("f_27_", seq(1, 10, 1)), sep = seq(1,10,1)) |> 
  pivot_longer(cols = starts_with("f_27_"), names_to = "column", values_to = "letter") |> 
  count(column, letter, target) |> 
  ggplot(aes(x = letter, y = n, fill = target))+
  geom_col(position = "identity", alpha = 0.5)+
  scale_fill_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  scale_y_continuous(label = scales::comma) +
  facet_wrap(~column, scales = "free")+
  labs(title = "Distribution f_27 (letters) vs target",
       x = "Value for each letter position",
       y = "Count",
       fill = "Machine\nstate") +
  theme_light()

A la vue de la distribution pour chaque position dans la chaine de caractère, ça ne fait aucun doute, il faut traiter la variable f_27 comme 10 variables différentes. De plus, il existe des différences plus marquées dans la distribution de ces variables entre les deux états, ce qui indique que ces variables seront probablement déterminantes pour prédire l’état.

Découverte d’interactions

Comment trouver des interactions ?

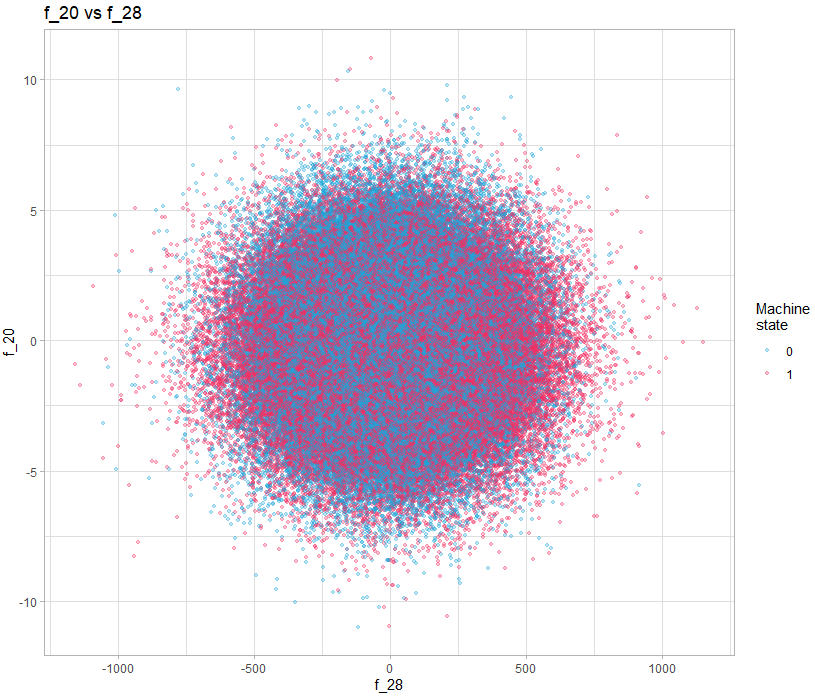
Une solution simple est de simplement visualiser les paires de variables, par exemple :

train |> 
  sample_n(size = 200000) |> 
  select(target, f_20, f_28) |> 
  mutate(target = as.factor(target)) |> 
  ggplot(aes(f_28, f_20, color = target)) + 
  geom_point(alpha = 0.3, size = 0.9) +
  scale_color_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  labs(title = "f_20 vs f_28",
     x = "f_28",
     y = "f_20",
     color = "Machine\nstate") +
  theme_light()

Sur cet exemple, il n’y a rien d’évident, mais si on le fait pour toutes les variables, peut-on découvrir des motifs intéressants ? Oui vous avez bien lu, regarder toutes les paires de variables, avec 40 variables, ça demande de faire 1600 visualisations. C’est là qu’un langage comme R donne toute sa puissance, car bien entendu on va générer toutes les visualisations en automatique et de façon structurée pour qu’elles soient facile à regarder.

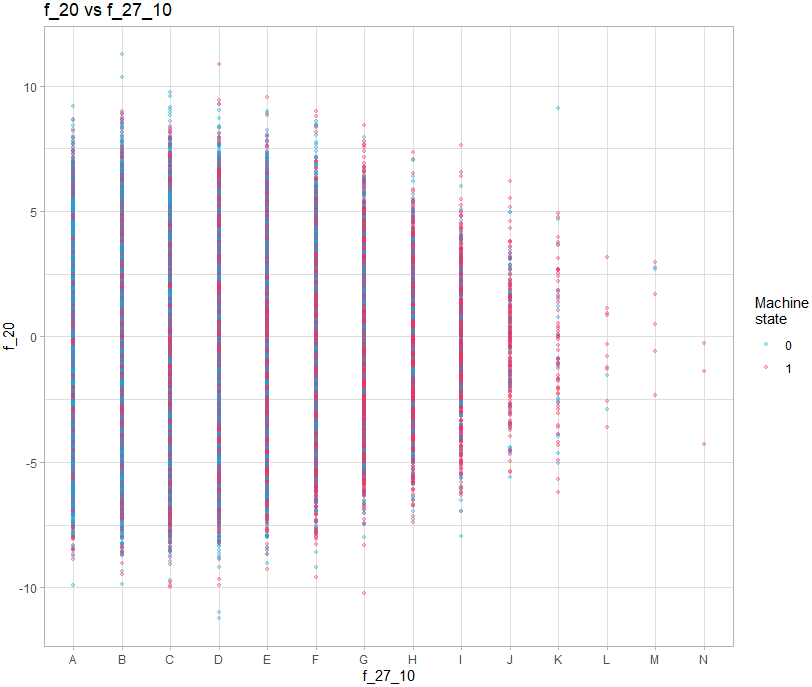
Pour les graphs contenant une variable discrete, toutes les observations vont se superposer sur la valeur de la variable :

train |> 
  sample_n(size = 200000) |> 
  separate(col = f_27, into = paste0("f_27_", seq(1, 10, 1)), sep = seq(1,10,1)) |> 
  select(target, f_20, f_27_10) |> 
  mutate(target = as.factor(target)) |> 
  ggplot(aes(f_27_10, f_20, color = target)) + 
  geom_point(alpha = 0.3, size = 0.9) +
  scale_color_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  labs(title = "f_20 vs f_27_10",
     x = "f_27_10",
     y = "f_20",
     color = "Machine\nstate") +
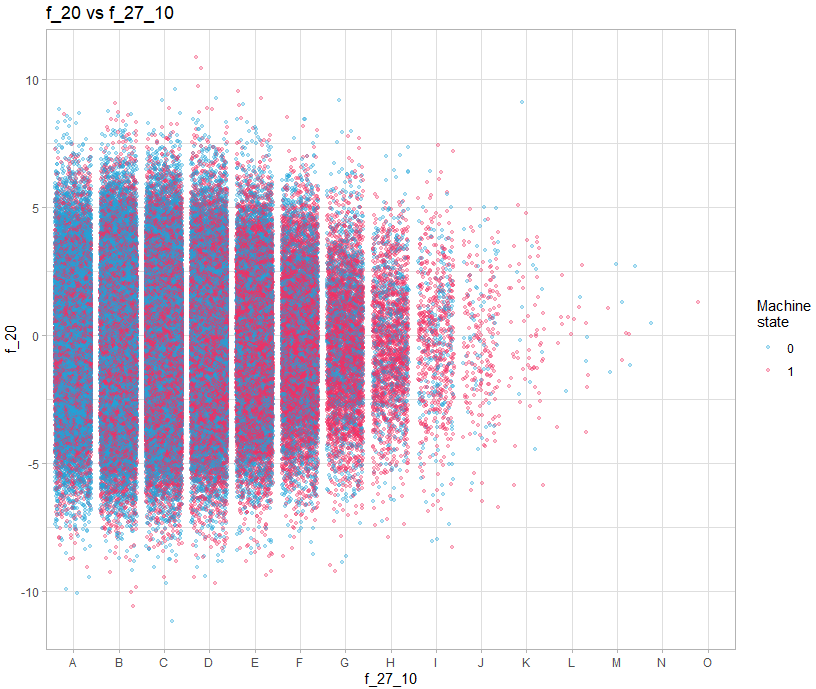
  theme_light()

Il faut donc ajouter un décalage aléatoire sur l’axe de la valeur discrete :

train |> 
  sample_n(size = 200000) |> 
  separate(col = f_27, into = paste0("f_27_", seq(1, 10, 1)), sep = seq(1,10,1)) |> 
  select(target, f_20, f_27_10) |> 
  mutate(target = as.factor(target)) |> 
  ggplot(aes(f_27_10, f_20, color = target)) + 
  geom_jitter(alpha = 0.3, size = 0.9, width = 0.4) +
  scale_color_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  labs(title = "f_20 vs f_27_10",
     x = "f_27_10",
     y = "f_20",
     color = "Machine\nstate") +
  theme_light()

On doit donc faire 3 types de graph :

Continue / continue
Continue / discrete (avec décalage sur l’axe de la variable discrete)
Discrete / discrete (avec décalage sur les deux axes)

Le script pour générer tous les graphs est disponible sur le dépôt github, mais voici le fonctionnement sur celui incluant les variables discretes et le décalage :

couples_graph_jit_save <- function(data, col1, col2, n = 500, jit_width = 0.4, jit_height = 0.4){

  file_name = glue::glue("graph_{col1}_{col2}.png")
  subdir = col1
  
  col1 <- sym(col1)
  col2 <- sym(col2)
  
  p <- data |> 
    sample_n(n) |> 
    ggplot(aes({{col1}}, {{col2}}, color = as.factor(target)))+
    geom_jitter(alpha = 0.3, size = 0.1, width = jit_width, height = jit_height)+
    scale_color_manual(values = c("0" = "#0477BF", "1" = "#D95B96")) +
    labs(title = glue::glue("variable {col1} vs {col2}"))+
    theme_light()
  
  if(!file.exists(here::here("graphs", subdir))){
    dir.create(file.path(here::here("graphs"), subdir))
  }
  
  ggsave(here::here("graphs", subdir, file_name), p, device = "png", dpi = 150, width = 5, height = 5)

}

Pour l’utiliser, on créé une grille contenant toutes les combinaisons de variables, avec la fonction walk2 du package purrr, on appelle la fonction avec les deux variables à utiliser en paramètre.

La fonction crée les différents graphiques dans des sous-répertoires du répertoire “graphs” qui sera créé pour l’occasion dans le répertoire du projet s’il n’existe pas au préalable.

La fonction peut n’utiliser qu’un échantillonage des données pour accélérer la création des graphiques et prend en paramètre les valeurs de décalages pour chaque axes.

Ainsi pour créer les graphiques pour les 10 variables issues de f_27 et toutes les variables continues :

col1 <- c("f_27_1", "f_27_2", "f_27_3", "f_27_4", "f_27_5", "f_27_6", "f_27_7", "f_27_8", "f_27_9", "f_27_10")
col2 <- c("f_00","f_01", "f_02", "f_03", "f_04", "f_05", "f_06", "f_19", "f_20", "f_21", "f_22", "f_23", "f_24", "f_25", "f_26", "f_28", "f_29", "f_30")

all_couples <- expand.grid(col1 = col1, col2 = col2, stringsAsFactors = FALSE) |> 
  filter(col1 != col2) |> 
  mutate(across(everything(), as.character))

walk2(all_couples$col1, all_couples$col2, ~couples_graph_jit_save(train, .x, .y, n = 900000, jit_width = 0.4, jit_height = 0))

On peut ensuite aller dans le répertoire “graphs” pour parcourir rapidement tous les graphs.

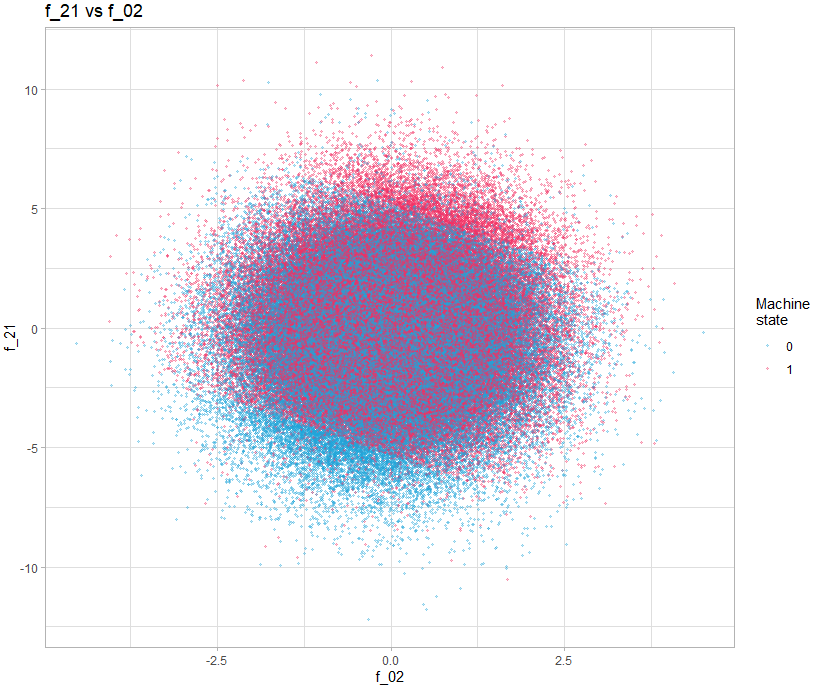
On s’aperçoit alors que certains présentent des motifs intéressants, par exemple le graph montrant f_21 vs f_02.

train |> 
  sample_n(size = 200000) |> 
  select(target, f_02, f_21) |> 
  mutate(target = as.factor(target)) |> 
  ggplot(aes(f_02, f_21, color = target)) + 
  geom_point(alpha = 0.3, size = 0.8) +
  scale_color_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  labs(title = "f_21 vs f_02",
     x = "f_02",
     y = "f_21",
     color = "Machine\nstate") +
  theme_light()

On voit clairement 3 zones délimités nettement par une ligne. L’idée d’additionner ces deux variables a été proposé dans le post suivant : https://www.kaggle.com/competitions/tabular-playground-series-may-2022/discussion/323892

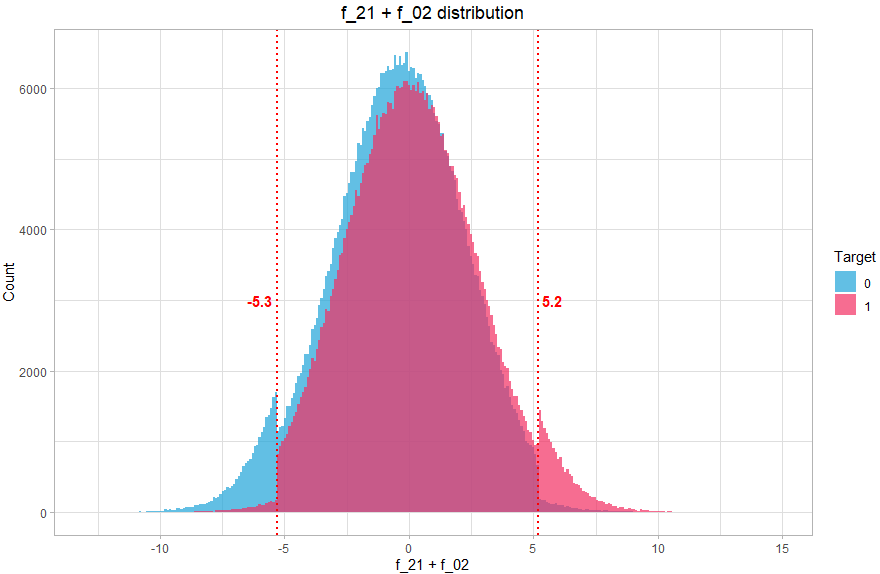
On créer alors une nouvelle variable qui va contenir 3 valeurs (-1, 0, 1) correspondante aux 3 zones. Comment trouver ces valeurs ? Là encore, on peut le faire graphiquement, en visualisant la distribution de la somme des deux variables :

train |> 
  mutate(f_inter = f_02 + f_21) |> 
  ggplot(aes(f_inter, fill = as.factor(target))) +
  geom_histogram(alpha = 0.7, position = "identity", bins = 300) +
  geom_vline(xintercept = -5.3, size = 0.8, color = "red", linetype = "12") +
  geom_vline(xintercept = 5.2, size = 0.8, color = "red", linetype = "12") +
  annotate("text", x = -5.3, y = 3000, label = "-5.3", hjust = 1.2, color = "red", fontface = "bold") +
  annotate("text", x = 5.2, y = 3000, label = "5.2", hjust = -0.2, color = "red", fontface = "bold") +
  scale_fill_manual(values = c("0" = "#1EA4D9", "1" = "#F22E62"))+
  labs(fill = "Target",
       title = "f_21 + f_02 distribution",
       x = "f_21 + f_02",
       y = "Count") +
  theme_light() + 
  theme(plot.title = element_text(hjust = 0.5))

On voit clairement que la distribution comprend 3 parties distinctes, on va donc associer 3 valeurs, la valeur -1 si f_21+f_02 < -5.3 (majoritairement class 0), 1 si f_21+f_02 > 5.2 (majoritairement class 1) et la valeur 0 sinon (équilibré).

Cette nouvelle variable permet de prendre en compte l’interaction découverte visuellement, et va aider à donner un boost à l’algorithme de classification.

Le principe est similaire pour les autres variables.

Création du modèle

Note : je ne vais pas ici expliquer le fonctionnement du deep learning, mais montrer l’architecture utilisée avec Keras pour notre cas précis. Je ne rentre pas non plus dans le détail de la cross validation, le code intégral est disponible sur github.

Ok on a trouvé graphiquement quelques informations, créé des nouvelles variables, mais comment s’en sert-on pour prédire l’état de la machine ?

On va utiliser Keras pour construire et entrainer un réseau de neurone, avec une couche d’entrée de la taille du nombre de variables, et en sorti 1 seul neurone avec une fonction d’activation « sigmoid » qui va permettre d’obtenir les probabilités (donc entre 0 et 1) que le statut soit 1. Entre les deux, on empile des couches cachées, dont la structure a été définie par cross validation pour différents essais d’architecture, jusqu’à trouver la combinaison qui donne les meilleurs résultats.

La structure du réseau retenu est donc la suivante :

Model: "sequential"
__________________________________________________________________
 Layer (type)          Output Shape            Param #            
==================================================================
 dense_4 (Dense)       (None, 64)              2880               
 dense_3 (Dense)       (None, 64)              4160               
 dense_2 (Dense)       (None, 64)              4160               
 dense_1 (Dense)       (None, 16)              1040               
 dense (Dense)         (None, 1)               17                 
==================================================================
Total params: 12,257
Trainable params: 12,257
Non-trainable params: 0
__________________________________________________________________

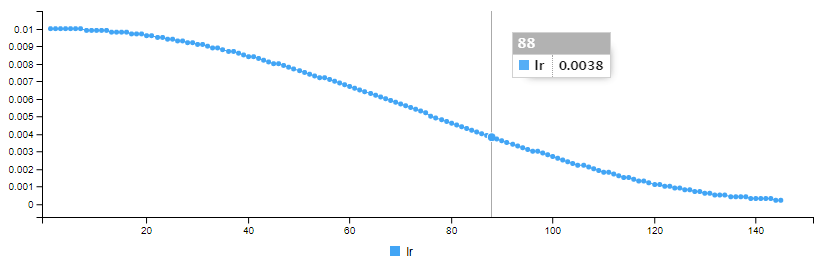
Comme beaucoup d’algorithme d’apprentissage automatique, un réseau de neurone utilise un taux d’apprentissage, et au lieu d’utiliser un taux fixe, on va faire décroire le taux en définissant une fonction qui va donner au taux d’apprentissage une forme de cosinus en fonction du nombre d’epoch :

La fonction cosine_decay() pour faire varier le taux d’apprentissage est définie comme ci-dessous :

EPOCHS_COSINEDECAY <- 150
CYCLES <- 1

cosine_decay <- function(epoch, lr){
  lr_start <- 0.01
  lr_end <- 0.0002
  epochs <- EPOCHS_COSINEDECAY
  
  epochs_per_cycle <- epochs %/% CYCLES
  epoch_in_cycle <- epoch %% epochs_per_cycle
  
  if(epochs_per_cycle > 1){
    w = (1 + cos(epoch_in_cycle / (epochs_per_cycle-1) * pi)) / 2
  }else{
    w = 1
  }
  return(w * lr_start + (1 - w) * lr_end)
}

Nous utilisons pour chaque couche cachée une fonction d’activation “swish” et pour la couche de sortie une fonction d’activation “sigmoid”. Enfin nous ajoutons une régularisation L2 pour les couches cachées.

Mis ensemble, le modèle se définit avec R et Keras comme suit :

model <- keras_model_sequential() %>% 
  layer_dense(units = 64, activation = "swish", input_shape = c(length(train_df)), kernel_regularizer = regularizer_l2(l = 30e-6)) %>% 
  layer_dense(units = 64, activation = "swish", kernel_regularizer = regularizer_l2(l = 30e-6)) %>%
  layer_dense(units = 64, activation = "swish", kernel_regularizer = regularizer_l2(l = 30e-6)) %>%
  layer_dense(units = 16, activation = "swish", kernel_regularizer = regularizer_l2(l = 30e-6)) %>% 
  layer_dense(1, activation = "sigmoid")

Nous utilisons l’optimiseur « adam », définit comme suit:

optimizer <- optimizer_adam(learning_rate = 0.01)

Il nous faut à présent compiler le modèle, en passant les paramètres du modèles, pour la fonction de perte, s’agissant de classification binaire, on utilise « binary_crossentropy » et comme métrique on utilise « AUC » qui est l’évaluation utilisée pour la compétition.

model %>% 
  compile(
    loss = "binary_crossentropy",
    optimizer = optimizer,
    metrics = "AUC"
  )

On peut alors entrainer le modèle avec la fonction fit(), en passant en paramètre, une matrice contenant les données d’entrainement, le statut des données d’entrainement (la classe à prédire), epoch, batchsize et le pourcentage pour les données de validation.

On défini également deux fonction de callback, une pour indiquer d’utiliser la fonction cosine_decay, et une pour arrêter prématurement l’apprentissage (early stopping) si la perte du jeu de validation ne s’est pas améliorée pendant 12 epochs.

model %>% fit(
     train_mx, 
     train_target, 
     epochs = 150, 
     batch_size = 4096, 
     validation_split = 0.1,
     callbacks = list(
       callback_early_stopping(monitor='val_loss', patience=12, verbose = 1, mode = 'min', restore_best_weights = TRUE),
       callback_learning_rate_scheduler(cosine_decay)
     )
 )

Keras produit les données d’entrainement pour chaque epoch (perte et auc pour les données d’entrainement et de validation, ainsi que le taux d’apprentissage)

Epoch 1/150
178/178 [==============================] - 5s 23ms/step - loss: 0.2217 - auc: 0.9722 - val_loss: 0.1469 - val_auc: 0.9884 - lr: 0.0100
Epoch 2/150
178/178 [==============================] - 3s 16ms/step - loss: 0.1274 - auc: 0.9913 - val_loss: 0.1191 - val_auc: 0.9925 - lr: 0.0100
.
.
.
Epoch 144/150
178/178 [==============================] - 3s 15ms/step - loss: 0.0565 - auc: 0.9984 - val_loss: 0.0675 - val_auc: 0.9975 - lr: 2.3916e-04
Epoch 145/150
178/178 [==============================] - 3s 15ms/step - loss: 0.0565 - auc: 0.9984 - val_loss: 0.0674 - val_auc: 0.9975 - lr: 2.2720e-04h: 133.
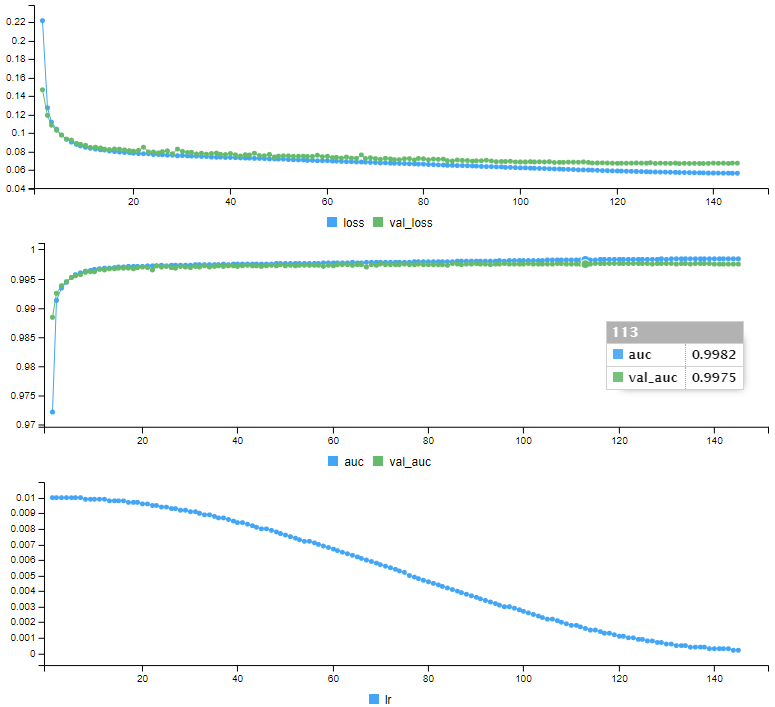
Epoch 145: early stopping

Ainsi qu’une série de courbes montrant l’évolution de chaque indicateur au fil de l’entrainement:

Notre modèle est entrainé, il est prêt pour faire des prédictions. Avant de prédire les données de test dont on ne connait pas le statut, on va effectuer des prédictions sur les données de validation, dont on pourra comparer les prédictions avec le statut réel :

On utilise la fonction predict() :

statut_proba <- model %>% predict(as.matrix(validTransformed))

Qui contient bien des probabilités pour chaque observation :

> head(statut_proba)
             [,1]
[1,] 9.954630e-01
[2,] 2.310278e-07
[3,] 3.195361e-05
[4,] 5.789851e-09
[5,] 9.999977e-01
[6,] 3.583938e-05

On calcule alors l’AUC :

predictions <- tibble(target = valid_target, prob = statut_proba[,1])
roc_may <- roc(predictions$target, predictions$prob)
auc(roc_may)

Area under the curve: 0.9979

Qu’est-ce que ça donne en terme de prédiction ?

Pour que ce soit plus facile à visualiser, nous transformons les probabilité en classe en prenant comme seuil de probabilité 0.5 (tout ce qui est inférieur à 0.5 est de statut 0, ce qui est au dessus est de statut 1), et nous pouvons visualiser la matrice de confusion :

          Truth
Prediction     0     1
         0 45484  1020
         1   927 42569

Sur 90 000 observations des données de validation, l’algorithme a prédit le bon statut pour 88053 observations. Il y a 1020 faux négatif et 927 faux positif, ce qui correspond à 97,83 % de prédictions correctes.

En soumettant les prédictions du jeu de test sur Kaggle, l’AUC est de 0.99819

Conclusion

Cet exemple montre que même avec des données qui au premier abord paraissent difficilement exploitable, nous sommes capables de faire de bonnes prédictions en combinant des découvertes lors de l’analyse des données et la capacité du deep learning à trouver des interactions.

L’utilisation d’une bibliothèque comme Keras rend la tâche plus simple puisque l’API est claire et orientée sur la productivité, nous pouvons nous concentrer sur l’expérimentation. Cela permet de voir également que R est un langage qui n’a pas à rougir face à Python puisqu’il permet d’utiliser les mêmes bibliothèques de deep learning (Keras, TensorFlow et Torch) et d’obtenir les mêmes résultats.